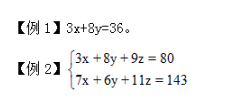在行测数量关系中,不定方程是常考知识点,但这类题型颇有难度,上海公务员考试网在此为大家进行展开分析。
不定方程的含义
未知数个数多于独立方程个数的方程,那么这样的方程我们就称为不定方程。
不定方程的求解
对于不定方程,实际上每一个x都有对应的y的值,那么具体我们怎么去解题呢?因为数量关系都是选择题,因此只有一个选项,所以我们最原始的方法就是带入排除法。但是如果正确的答案是D,做题时间就会比较长。所以我们应该学会先排除后代入,接下来具体介绍几种代入方法。
1、整除法
当未知数的系数和常数项之间存在着公约数,此时我们考虑采用整除的方法。
例题
3x+7y=49,已知x、y为正整数,则x=( )
A.4 B.7 C.9 D.11
【答案】B。解析:由题可知,7y和49都能被7整除,则3x也能被7整除,即x能被7整除,结合选项,选择B。
2、奇偶性法
当未知数前面的系数奇偶互异,此时我们考虑采用奇偶性的方法。
例题
3x+6y=42,已知x、y为正整数且x为质数,则x=( )
A.2 B.3 C.6 D.7
【答案】A。解析:由题可知,6x和42均为偶数,则3x为偶数,即x为偶数且为质数,结合选项,则x=2,选择A项。
3、尾数法
当未知数前面的系数是5或者5的倍数,此时我们考虑采用尾数的方法。
例题
3x+10y=49,已知x、y为正整数,则x=( )
A.1 B.3 C.5 D.7
【答案】B。解析:由题可知,10y的尾数为0,49的尾数为9,则3x的尾数必须为9,结合选项,则x=3,选择B项。