说起浓度问题,很多人就开始皱起眉头,一种“题不醉人人自醉”的感觉,可是浓度问题真的有那么可怕吗?其实并不,在解决浓度问题的时候,只要把握几个关键点,很多题目都可以迎刃而解。那什么是浓度问题呢,其实不止是在数量关系题目中,生活中也经常会碰到浓度问题,回想下自己买奶茶的时候,是不是经常被问到,是要少糖,中糖,还是多糖?其实奶茶小哥就是在问你浓度的问题,你是要糖的浓度低一点还是高一点呢?没想到吧!所以浓度问题无所不在,而浓度问题也很简单,浓度的基本公式为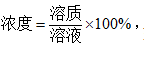 如一杯糖水的浓度指的就是溶质(糖)的量/溶液(糖水)的量,也就是浓度越高,也就越甜。
如一杯糖水的浓度指的就是溶质(糖)的量/溶液(糖水)的量,也就是浓度越高,也就越甜。
那接下来我们就来研究一下,浓度问题在数量关系当中如何快速求解吧!
例1
有两瓶质量均为1千克的酒精溶液,浓度分别为70%和45%,先从两瓶中各取部分混合成1千克的酒精溶液,测得浓度恰好为50%,再将这两瓶中剩下的溶液混合,则所得酒精浓度是:
A.50% B.55% C.60% D.65%
【解析】D。两瓶溶液的溶质质量分别为1×70%=0.7千克、1×45%=0.45千克,第一次取出混合后的1千克溶液中含有溶质1×50%=0.5千克,则余下溶液混合后含有溶质0.7+0.45-0.5=0.65千克,而溶液剩余1千克,即浓度为0.65÷1×100%=65%。选择D选项。
总结:不管溶液怎么混合,浓度基本公式要记牢,让最终求浓度,就找所需溶质和溶液的量,若能直接表示出所需溶质和溶液的量,即可直接求解。
例2
在一杯清水中放入10克盐,然后再加入浓度为5%的盐水200克,这时配成了浓度为2.5%的盐水,问原来杯中有清水多少克?
A.460克 B.490克 C.570克 D.590克
【解析】D。设原来杯中有清水x克,则根据混合前后溶质总量不变,可得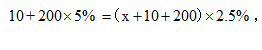 ,解得x=590。选择D选项。
,解得x=590。选择D选项。
总结:如果不能直接求解所求量,把握一点,即不管有多少溶液混合在一起,就结合混合前后溶质和溶液总量不变,列方程,大多即可迎刃而解。
总结:溶液混合问题除了根据溶质,溶液总量不变列方程,也可根据十字交叉求解,两部分浓度写左边,整体浓度写中间,沿着十字线作差,差值的比值即为两部分对应溶液量的比值。


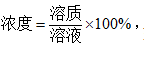 如一杯糖水的浓度指的就是溶质(糖)的量/溶液(糖水)的量,也就是浓度越高,也就越甜。
如一杯糖水的浓度指的就是溶质(糖)的量/溶液(糖水)的量,也就是浓度越高,也就越甜。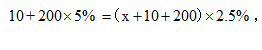 ,解得x=590。选择D选项。
,解得x=590。选择D选项。