几何问题是近几年国、联考中必考的热门题型,考查频率越来越高。其中的最短路径问题考查较多,方法性很强,通过学习可以有良好掌握,学习的性价比很高。下面公职资讯网为大家具体讲解如何解决几何中的最短路径问题。
最短路径问题考查形式通常为求点之间的最短距离,核心解题方法为平面上两点之间,线段最短。在考试中最短路径问题主要分为两大类,平面几何最短路径与立体几何最短路径。虽然题目有多种问法,但万变不离其宗,只要知识点掌握牢固、能够融会贯通,无论如何创新如何结合,我们都可以熟练解决。
平面几何最短路径问题
1.两点异侧
题型特征:求在直线异侧的两点之间的最短距离,或在直线异侧的两点到第三点的最短距离之和
解题方法:两点之间,线段最短,三点共线时距离之和最短
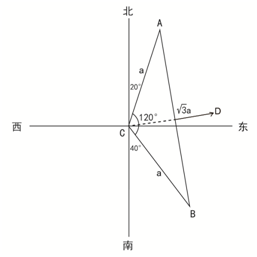
例1.【2011联考】火车站A和B与初始发车站C的直线距离都等于akm,站点A在发车站C的北偏东20度,站点B在发车站C的南偏东40度,若在站点A和站点B之间架设火车轨道,则最短的距离为:
A. akm
B. 3akm
C. 2akm
D. 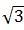 akm
akm
【解题思路】如图所示,根据题意中A在C点北偏东20度和B在C点南偏东40度可知,A、B、C三点构成顶角为120度的等腰三角形,且AB为底边。过点C做AB的中垂线,交AB于点D。根据勾股定理可得,CD=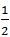 a,AD=
a,AD=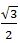 a,则AB=2AD=
a,则AB=2AD=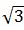 a,正确答案为D。
a,正确答案为D。
【点评】公务员考试中,三角形求边长常用勾股定理和相似三角形。因此建议各位考生将常见三角形边长比例熟练记忆,如30°直角三角形、等腰直角三角形、120°等腰三角形等。本题若变形为C火车站正东建立新火车站D,求AB两点到D距离之和最短,因三点共线时距离之和最短,直接连接AB即为最短距离和。
2.两点同侧
题型特征:求在直线同侧的两点到第三点的最短距离之和
解题方法:将其中一点镜像对称,使三点共线
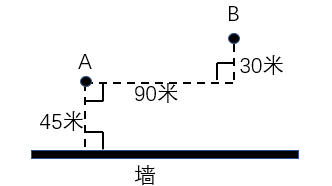
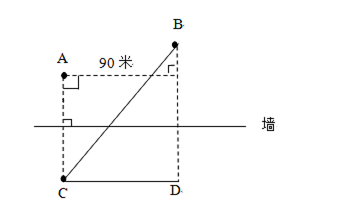
例1.【2019浙江】 A、B点和墙的位置如图所示。现从A点出发以5米/秒的速度跑向墙,接触到墙后再跑到B点。问最少要多少秒到达B点?
A. 30
B. 34
C. 38
D. 42
【解题思路】要用最短时间到达B点,在速度一定的情况下,需从A接触到墙后再跑到B点所走的路程最短。如图,由于A和B在墙的同侧,可考虑做其中一个点关于墙的对称点,该对称点与另一个点的连线即为最短路程。假设做A点的对称点C,最短距离为BC。CD=90米,BD=30+45+45=120米,BC=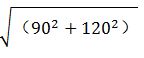 =150米,则t=
=150米,则t=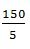 =30秒,正确答案为A。
=30秒,正确答案为A。
【点评】先判断为同侧问题,需要作其中一点的对称点,再连接另外一点,用勾股定理求解。两点同侧时,对称哪一个点都可以,但是一般为了计算方便,建议对称短的那一个。
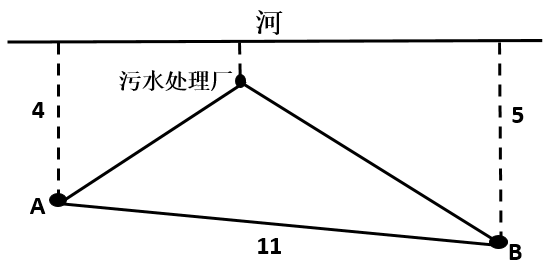
例2.【2017联考】如下图所示,某条河流一侧有A.、B.两家工厂,与河岸的距离分别为4km和5km,且A.与B.的直线距离为11km。为了处理这两家工厂的污水,需要在距离河岸1km处建造一个污水处理厂,分别铺设排污管道连接A.、B.两家工厂。假定河岸是一条直线,则排污管道总长最短是:
A. 12km
B. 13km
C. 14km
D. 15km
【解题思路】如下图所示,过污水处理厂做河岸的平行线HC,D为A关于HC的对称点,则最短距离为DB,由题污水厂离河1km可得A点距离到HC为HA=HD=3km,B点距离HC等于EH=4km,则DE=3+4=7km。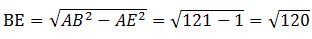 ,所以
,所以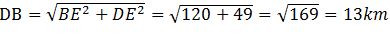 ,正确答案为B。
,正确答案为B。
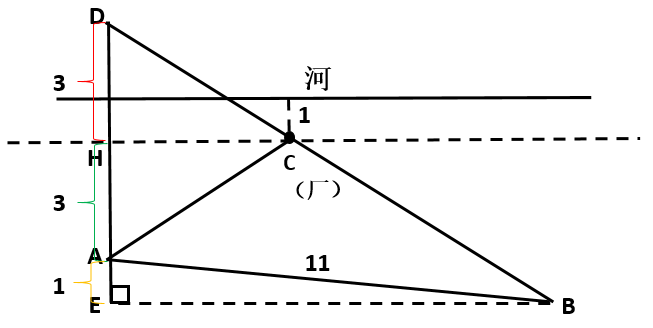
【点评】本题中题目AB为河流一侧,因此为两点同侧。提醒大家注意,若以河为对称轴,求的点为交点,此时污水处理厂建在河里,因此此题的对称轴是第三个点所在的水平线,过C作一条沿河岸的平行线,轴距离河岸为1km。计算时若忽略了这一点,将无法求解正确答案。
立体几何最短路径问题
题型特征:求立体图形中两点的最短距离
解题方法:将立体图形展开放在同一平面,连线计算
例1.【2019河北】长、宽、高分别为12cm、4cm、3cm的长方体ABCD-A_1 B_1 C_1 D_1上,有一个蚂蚁从A出发沿长方体表面爬行到C_1获取食物,其路程最小值是多少cm?
A. 13
B.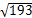
C.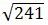
D. 17
由题干蚂蚁从A出发沿长方体表面爬行到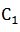 求
求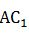 最短,画图可知,在长方体中A和
最短,画图可知,在长方体中A和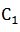 不在同一平面,要求最短距离先要把A和C_1放在同一平面内,则把面
不在同一平面,要求最短距离先要把A和C_1放在同一平面内,则把面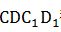 翻折,形成面
翻折,形成面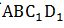 ,再连接
,再连接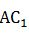 ,根据两点之间直线最短求解。如下图:
,根据两点之间直线最短求解。如下图:
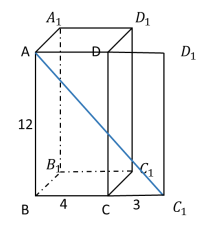
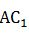 是直角三角形ABC_1的斜边,要让斜边最短,则两直角边的平方和要尽可能小。当AB=12,
是直角三角形ABC_1的斜边,要让斜边最短,则两直角边的平方和要尽可能小。当AB=12,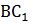 =4+3=7时,两直角边的平方和最小,
=4+3=7时,两直角边的平方和最小,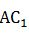 最短=
最短=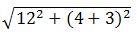 =
=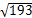 ,正确答案为B。
,正确答案为B。
【点评】长方体最短路径问题可直接运用结论,长方体中相对的两个顶点沿表面走的最短距离为: ;最短路径数为2条,因为长方体存在对立面,每一条路径都有一条与之相对的路径,因此有2条。
;最短路径数为2条,因为长方体存在对立面,每一条路径都有一条与之相对的路径,因此有2条。
例2. 【2013北京】A和B为正方体两个相对的顶点,一个点从A出发沿正方体表面以最短路径移动到B,则其可选择的路线有几条:
A. 2
B. 3
C. 6
D. 12
【解题思路】正方体有3组对立面,如图可知每一条路线在对立面上都有一条与之对应的路线,因此每组对立面有2条路线,3组对立面共6条路线,正确答案为C。
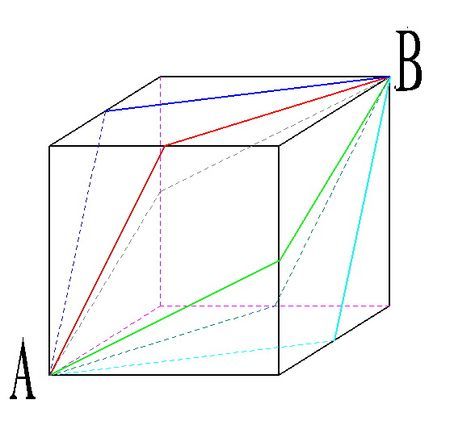
【点评】若本题为求A到B最短距离,则可将正方体展开,将AB放在同一平面内。连接AB后,AB=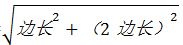 =
=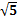 边长。
边长。
正方体最短路径问题也有有对应结论,小编建议可以直接用结论做题,正方体中相对的两个顶点最短距离为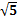 边长,最短路径数为6条。
边长,最短路径数为6条。
以上就是对于几何中的最短路径问题的详细讲解。几何问题在近几年的国考、联考及单独命题省考中每年均有考查,最短路径问题大家可以看到套路性很强,希望各位考生通过学习均能对此有良好的掌握。


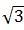 akm
akm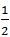 a,AD=
a,AD=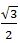 a,则AB=2AD=
a,则AB=2AD=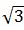 a,正确答案为D。
a,正确答案为D。

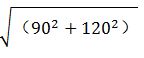 =150米,则t=
=150米,则t=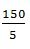 =30秒,正确答案为A。
=30秒,正确答案为A。

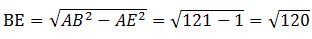 ,所以
,所以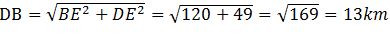 ,正确答案为B。
,正确答案为B。
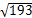
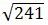
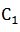 求
求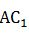 最短,画图可知,在长方体中A和
最短,画图可知,在长方体中A和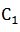 不在同一平面,要求最短距离先要把A和C_1放在同一平面内,则把面
不在同一平面,要求最短距离先要把A和C_1放在同一平面内,则把面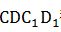 翻折,形成面
翻折,形成面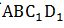 ,再连接
,再连接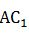 ,根据两点之间直线最短求解。如下图:
,根据两点之间直线最短求解。如下图:
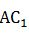 是直角三角形ABC_1的斜边,要让斜边最短,则两直角边的平方和要尽可能小。当AB=12,
是直角三角形ABC_1的斜边,要让斜边最短,则两直角边的平方和要尽可能小。当AB=12,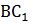 =4+3=7时,两直角边的平方和最小,
=4+3=7时,两直角边的平方和最小,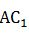 最短=
最短=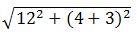 =
=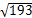 ,正确答案为B。
,正确答案为B。 ;最短路径数为2条,因为长方体存在对立面,每一条路径都有一条与之相对的路径,因此有2条。
;最短路径数为2条,因为长方体存在对立面,每一条路径都有一条与之相对的路径,因此有2条。
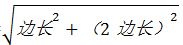 =
=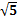 边长。
边长。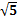 边长,最短路径数为6条。
边长,最短路径数为6条。