本期为各位考生带来了2018重庆公务员考试行测备考:几何问题中的最短线路问题。相信行测考试一定是很多考生需要努力攻克的一道坎儿。行测中涉及的知识面之广,考点之细,需要开始做到在积累的同时掌握一定的解题技巧。重庆公务员考试网温馨提示考生阅读下文,相信能给考生带来一定的帮助。
更多重庆公务员考试复习技巧详见 2018年重庆公务员考试通用教材
仔细研读下文>>>2018重庆公务员考试行测备考:几何问题中的最短线路问题
几何问题是行测考试中相对来说比较常考的问题,因为几何问题涉及到的知识点非常多,范围非常广泛,能够更全面的考察学员的能力。而在几何问题中,有一类题目是将几何问题和图形推理中的一笔画问题相结合的,那就是最短线路问题。那什么是最短线路问题呢?
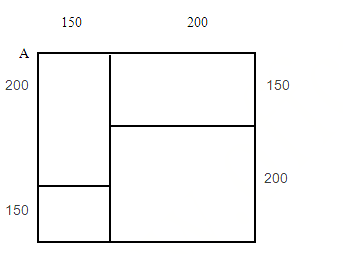
某社区道路如下图所示,社区民警早上9点整从A处的办公室出发,以每分钟50米的速度对社区内每一条道路进行巡查(要求完整走过整个社区内的每一段道路),问他最早什么时候能完成任务返回办公室?
想要解决这个问题,我们就得思考怎么走才能够才能保证走的距离最短,也就是最早回到办公室。因为题干中要求必需巡查每一条道路,所以如果能够按照一笔画图形去走的话应该是最短的。而且题干中要求要回到A点,那就还要考虑一笔画问题中的画法问题。
1.一笔画:当奇点的个数为0或者2时,这个图形可以由一遍画完成。
2.画法:当奇点的个数为0时,所有的点都是偶点,可以从任意点出发,完成一笔画并且回到原点;
当奇点的个数为2时,必须从奇点出发,回到另外一个奇点,才能完成一笔画。
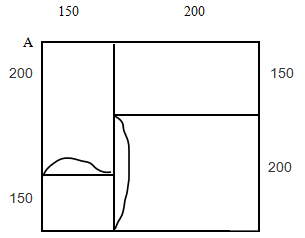
所以由以上的结论可知,先要构成一笔画,则奇点的个数必须为0或者2,而本题中要求回到原点,则奇点的个数必须为0。我们可以将某些奇点连接起来,将奇点的个数降为0,如图:
当然在连接的时候,还要尽量保证所连接的线段或者线段和是最小的,所以该民警走的最短距离为:350×4+350+350+150+200+250=2700米,最短时间:2700÷50=54分钟,回到办公室的最早时间是9点54分。
专家提醒:广大考生一定要注意各学科以及各知识点之间的联系,做题时才能更加得心应手。